Некоторые сайты, например новостные, не имеют явных целевых действий, таких как заказ или подписка. Для них важно не выполнение посетителем каких либо действий, а само присутствие посетителя на сайте, желательно регулярное. Но и для e-commerce сайтов тоже очень важны возвраты посетителей, так как вернувшийся посетитель обходится намного дешевле, чем новый. Каждый возврат это шанс что нибудь продать, при этом чем меньше интервал между возвратами, тем больше шансов на осуществление продажи.
Задача определения того, продолжит ли посетитель/клиент пользоваться сервисом, или ушёл и никогда больше не вернётся, называется churn prediction (прогнозирование оттока). Лобовой подход к её решению – взять определенный промежуток времени, например месяц или полгода, и спрогнозировать вероятность возврата клиента в этом промежутке. Обычно data scientist-ы так и поступают. Но такой подход не очень хорош с точки зрения качества прогноза.
Во-первых, хорошо бы использовать прогнозное значение, как метрику вовлечённости клиента (т.е. насколько он “churned” или “not churned”). Клиент, который вернётся на сайт завтра, очевидно, более вовлечён, чем клиент, который вернётся через полгода. Но для модели, определяющей просто вероятность возврата в течение полугода, оба клиента будут совершенно равнозначны.
Во-вторых, возникает вопрос выбора размера промежутка для прогноза. Каким он должен быть? Месяц? Квартал? Год? Интуитивно кажется, что чем больший период жизни клиента мы охватываем, тем лучше. Но если взять промежуток в год, то обучаться можно будет только на устаревших данных (старше года), так как данные за последний год будут использоваться только для формирования целевых значений. За год данные могут и “протухнуть”: изменится сам сайт, изменятся источники трафика и свойства аудитории. Чем свежее обучающие данные, тем качественнее будет прогноз.

Более правильным кажется предсказывать не вероятность возврата внутри фиксированного промежутка, а интервал времени до следующего посещения сайта, лежащий в диапазоне $[t_s, \infty]$, где $t_s$ это таймаут, которым разделяются сессии (8 часов). Чем меньше этот интервал, тем более вовлечён клиент. Если предсказанный интервал близок к бесконечности, то клиент возможно не вернётся на сайт никогда, и можно считать, что он churned. Порог, после которого клиент становится churned, можно выбирать и изменять уже после обучения модели, это ещё один плюс.
Но тогда возникает другая проблема: чему равен интервал для клиентов, которые ушли с сайта и пока не вернулись?
Ведь верхняя его граница находится где то в будущем (возможно, бесконечно далёком).
Точно известно только то, что этот интервал больше, чем now_time - last_event_time.
Как обучать модель, если целевая переменная определена только нижней границей?
Такое обучение возможно при использовании регрессионной модели, которая называется Cox Proportional Hazards. Чтобы понять, про какие “пропорциональные опасности” идет речь, надо немного познакомиться с анализом выживаемости (Survival analysis).
Survival analysis
Задача прогноза времени до наступления события (в нашем случае - возврата на сайт) встречается в жизни довольно часто, но теория анализа выживаемости и соответствующие методики прогнозирования сначала были разработаны для медицинских исследований. Событием, наступление которого анализировалось, являлась смерть пациента, отсюда и название “анализ выживаемости”. Такой анализ часто применяется при сравнении групп пациентов, получивших разные способы лечения: более эффективен тот способ, где пациенты прожили дольше. В нашем случае логика инвертируется: хороший клиент это тот, кто вернулся на сайт (“умер” с точки зрения survival analysis) как можно раньше.
Естественно, врачи не хотели дожидаться естественной смерти всех пациентов, чтобы сделать выводы об эффективности лечения. Поэтому survival analysis умеет работать с цензурированными (censored) данными. Цензурирование возникает, когда точное время наступления события неизвестно (находится где то в будущем, пациент все еще жив), известно только, что событие не наступило до определенного момента времени (обычно до текущего момента).
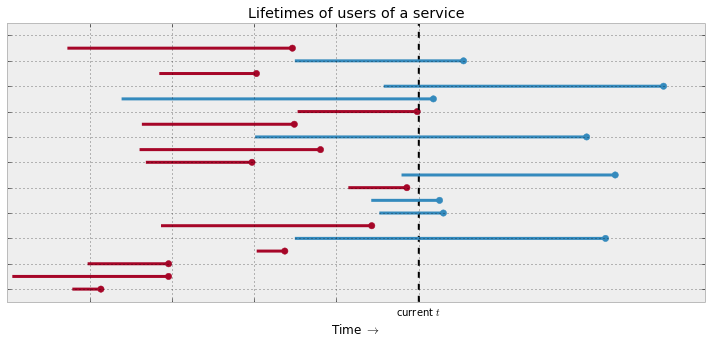
Времена до возврата на сайт. Бордовым показаны посетители, у которых время возврата уже известно, голубым - которые еще не вернулись (вернутся в будущем), у них цензурированное время наступления события.
Базовое понятие анализа выживаемости это Survival function (функция выживания): $$ S(t) = \Pr(T>t) $$ где $T$ – время жизни члена популяции, $t$ – произвольный интервал времени. Смысл функции – вероятность того, что член популяции проживёт дольше, чем $t$. Функция является строго убывающей, в момент времени $t=0$ вероятность равна 100% (все только что родились), по мере возрастания $t$ вероятность убывает (постепенно умирают). Для пациентов вероятность станет практически нулевой после 100 лет, но в общем случае возможна “вечная жизнь”, когда часть популяции выживает в течение всего обозримого времени (в нашем случае – клиент никогда не возвращается на сайт).
Давайте визуализируем функцию выживания разных когорт посетителей на сайте shop.ml. Когорты сформируем из тех, у кого была только одна (первая) сессия, две и три сессии, и посмотрим на динамику возвратов:
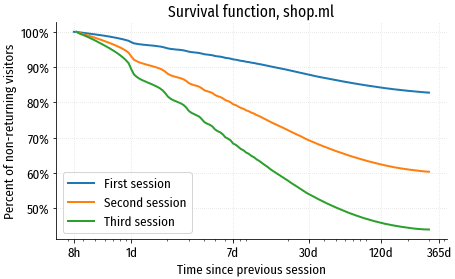
График функции выживаемости это по сути перевёрнутый график user retention. На старте есть 100% юзеров, постепенно часть из них возвращается, а часть теряется навсегда (графики заканчиваются выше нулевой точки). Посетители с единственной сессией возвращаются на сайт очень неохотно: за две недели возвращается только 10%, а в течение года количество вернувшихся не доходит даже до 20%. Посетители, у которых было уже две или три сессии намного более вовлечены: в течение недели возвращается 20% посетителей с двумя сессиями, а в течение двух месяцев – половина посетителей, у которых было три сессии.
Hazard function
Survival function показывает, какая доля популяции выживает (какая доля посетителей не возвращается) к моменту времени $t$. Комплементарная ей функция, lifetime distribution function, показывает, какая доля “умирает” к моменту $t$: $$F(t) = 1 - S(t)$$ Если взять производную от lifetime distribution function, получим плотность событий (количество смертей пациентов или возвратов посетителей) в единицу времени: $$f(t) = F’(t) = \frac{d}{dt}F(t)$$ Плотность событий не очень удобна для использования, т.к. по мере вымирания популяции общее количество событий быстро уменьшается. Поэтому обычно используют другую функцию, hazard function (функция риска), в которой количество смертей в единицу времени $f(t)$ нормируется на долю популяции, выжившей к этому моменту времени: $$\lambda(t) = \frac{f(t)}{S(t)} = -\frac{S’(t)}{S(t)}$$ Эта функция фактически показывает риск умереть в момент времени $t$ для тех, кто дожил до этого момента, отсюда название hazard function. Визуализируем функцию риска для наших когорт посетителей:
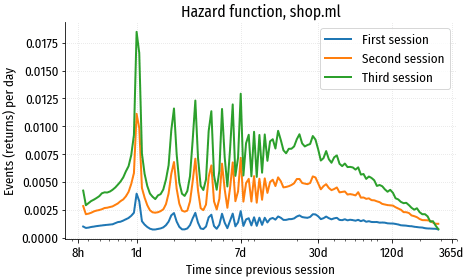
Используется также cumulative hazard function (кумулятивная функция риска), она выражает суммарный риск, накопившийся к моменту времени $t$: $$\Lambda(t)=\int_0^t\lambda(u) du$$ Cumulative hazard function и survival function связаны следующим выражением: $$S(t)=\exp(-\Lambda(t))$$
Cox proportional hazards
Одна из часто используемых в survival analysis моделей это Proportional hazards. В этой модели делается допущение, что функции риска для каждого индивидуального члена популяции имеют примерно одинаковую форму, задаваемую через общую для всех baseline hazard функцию $\lambda_0(t)$, и отличаются только на положительный коэффициент пропорциональности $k_i$, индивидуальный для каждого члена популяции: $$\lambda_i(t) = \lambda_0(t) k_i,\;i \in 1 \mathrel{{.}\,{.}} N $$ В классической модели, предложенной статистиком Дэвидом Коксом, коэффициент вычисляется с помощью линейной регрессии: $$k_i = \exp(logits_i)$$ $$logits_i = \mathbf{x_i}^\top\boldsymbol{\beta}$$ где $\mathbf{x_i}$ – вектор признаков i-го члена популяции, $\boldsymbol{\beta}$ – вектор коэффициентов линейной модели. Но ничего не мешает использовать для вычисления $logits$ любую другую модель машинного обучения, например нейросеть или деревья решений.
Изящество этой модели в том, её можно обучать через максимизацию частичного правдоподобия, не задавая в явном виде baseline функцию $\lambda_0(t)$, форма которой, вообще говоря, неизвестна до окончания обучения.
Допущение, что функции риска всех членов популяции отличаются только на пропорциональный коэффициент, конечно, не всегда соответствует реальности. В порядке эксперимента, попробуем привести функции риска для наших когорт посетителей к одному масштабу, умножая каждый график на эмпирически подобранный коэффициент. В идеале графики должны совпасть:
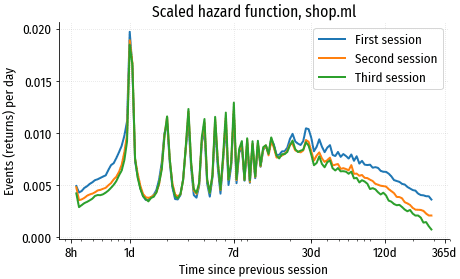
Графики в значительной степени совпадают, но не на 100%. Сильнее всего различается поведение после 30 дней.
В более продвинутых моделях каждый член популяции может иметь индивидуальную функцию риска произвольной формы. Но с другой стороны, чтобы смоделировать индивидуальные функции, требуется очень много обучающих данных, а proportional hazards модели хорошо работают даже на небольших обучающих выборках.
Моделирование
Пациент может умереть только единожды, поэтому survival analysis работает исключительно с с терминальными событиями, т.е. событие должно быть последней точкой в жизни члена популяции. В отличие от пациента, посетитель сайта может возвращаться неограниченное количество раз, поэтому мы немного схитрим, и представим, что каждая сессия происходит от лица виртуального нового посетителя. В этом случае модель может переобучиться на посетителях, которые возвращались много раз, т.к. их признаки будут учтены многократно. Чтобы этого не случилось, дадим каждому виртуальному посетителю вес $w_i = s_i^{-1}$, обратно пропорциональный количеству его сессий $s_i$.
В качестве метрики качества будем использовать уже знакомый по предыдущим статьям Concordance Index – обобщение метрики AUC для регрессионных задач. Важно, что Concordance Index корректно работает с цензурированными данными, ведь основной процент посетителей никогда не возвращается после первой сессии.
Модель Proportional Hazards выдаёт значение коэффициента $k_i$. С помощью Breslow estimator можно найти базовую кумулятивную функцию $\Lambda_0(t)$, и перейти от неё к функции выживания для i-го посетителя: $$S_i(t) = \exp\left(-\int_0^t k_i d\Lambda_0(u)\right)$$ Таким образом, результатом является не точечная оценка вероятного интервала между сессиями (как было бы в традиционных моделях), а целая вероятностная функция, параметризованная коэффициентом $k_i$.
Для скоринга посетителей по степени того, насколько они churned, абсолютные значения интервалов, и тем более вероятностные функции сложной формы не нужны. Достаточно значения коэффициента $k_i$: чем оно больше, тем более вовлечён (менее churned) посетитель. На практике удобнее использовать даже не сам коэффициент, а его логарифм (соответствующий $logits$ из модели), т.к. у логарифмического значения близкое к нормальному распределение, такие значения проще воспринимать.
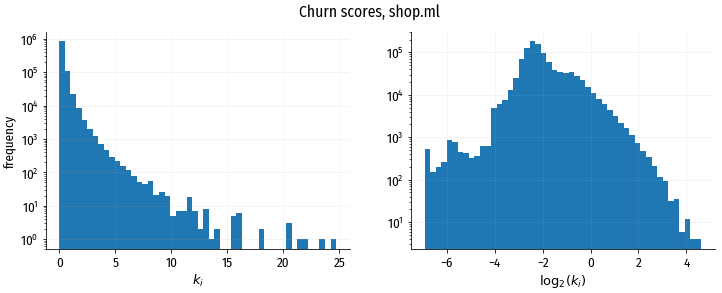
Слева распределение прогнозных значений коэффициента $k_i$, справа – распределение значений его логарифма. Правое распределение ближе к нормальному, левое – к экспоненциальному. Обратите внимание на логарифмическую шкалу частот (ось Y).
Shapely values рассчитываются тоже в этой логарифмической шкале. Одной единице шкалы соответствует двукратная разница в интенсивности событий “возврат на сайт”, т.е. за одинаковый промежуток времени на сайт вернётся в два больше раза посетителей из когорты, где $score=1$ по сравнению с когортой, где $score=0$.
Также обратим внимание, что распределение скоринговых значений зависит от того,
считается оно по уникальным посетителям или по уникальным сессиями (после каждой сессии
скоринговое значение обновляется):
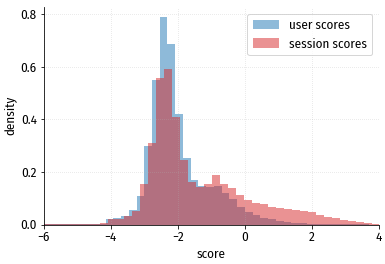
Если смотреть распределение по посетителям, кажется, что скоринговое значение $>2$ практически не встречается. Но в распределении по сессиям таких значений много, потому что активные посетители, у которых маленький промежуток между сессиями, генерируют в целом намного больше сессий, чем неактивные.
Результаты, shop.ml
Для начала, визуализируем получившуюся baseline hazard функцию, относительно
которой рассчитываются скоринговые коэффициенты:

Сюрпризов здесь нет, baseline повторяет форму функции риска, рассчитанную по исходным данным. Посмотрим, как будут отличаться функции выживания для посетителей с разными скоринговыми коэффициентами:
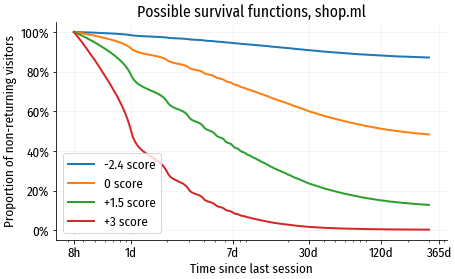
Половина посетителей с коэффициентом +3 вернётся на сайт уже на следующий день, а в течение года вернётся почти 100%. В то же время среди посетителей с коэффициентом -2.4 (самое распространённое значение в нашей выборке) даже через год на сайт возвращается только ~13%.
Concordance Index этой модели на тестовой выборке ~77%. С точки зрения классического machine learning это кажется довольно скромным результатом, но для survival analysis это хорошая точность. Ведь мы предсказываем по большому счёту случайную величину, зависящую от множества внешних факторов, которые невозможно учесть в модели.
Посмотрим, какие признаки играют определяющую роль в том, насколько
быстро посетитель вернётся на сайт:
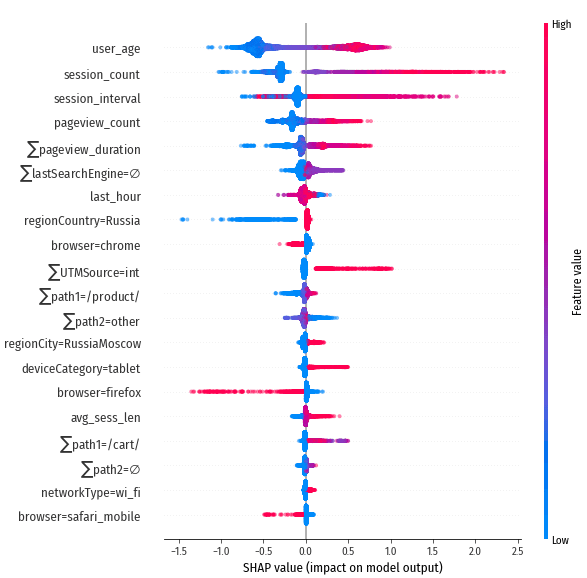
На первом месте – “возраст” user_age, т.е. насколько давно посетитель впервые появился на сайте.

На втором месте – session_count, количество сессий:
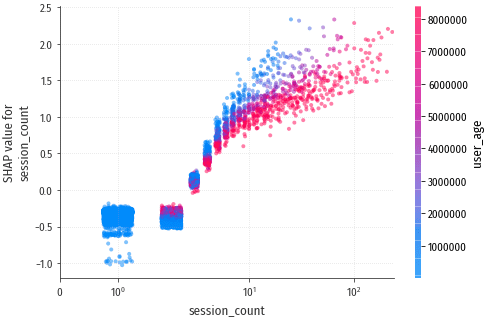
session_interval – средний промежуток времени между сессиями. Это
примерно то, что мы пытаемся прогнозировать, поэтому неудивительно, что
этот признак оказывает значительное влияние на результат:
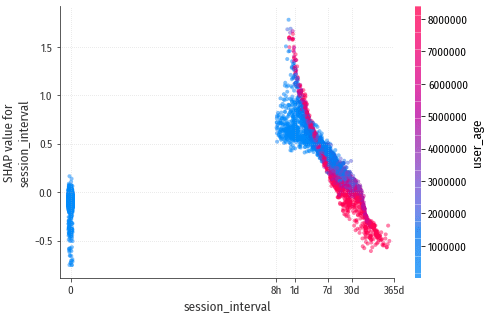
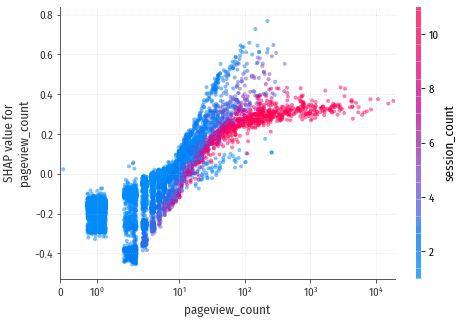
pageview_count – количество просмотренных страниц, также один из
главных показателей вовлечённости посетителя.
Результаты, другие сайты
Результаты работы модели на других сайтах весьма похожи на результаты
shop.ml, и отличаются только нюансами, связанными с разной структурой сайтов
и разной структурой входящего трафика. Поэтому не буду приводить подробные
результаты для каждого сайта, в качестве примера – summary для
courses.ml:
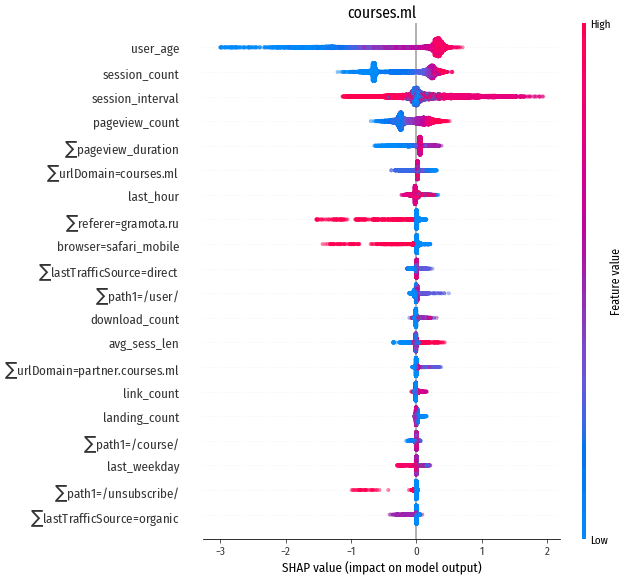
Точность по Concordance Index для всех сайтов находится в районе 75%. Форма baseline hazard function тоже довольно схожа у всех сайтов.
Индивидуальные прогнозы
Основное применение этой модели – прогнозирование вовлеченности
отдельных посетителей, чтобы работать с ними на индивидуальном уровне.
Поэтому здесь особенно важны scorecards, позволяющие “заглянуть в душу”
любого посетителя и получить представление о его планах на будущее.
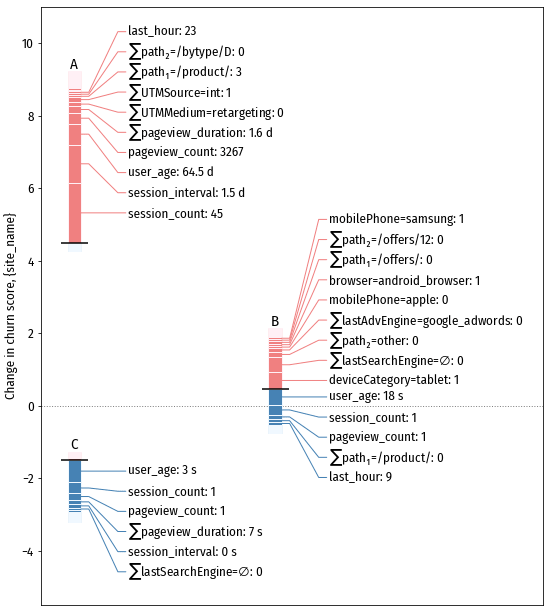
- A – посетитель, который по мнению модели точно вернётся на сайт в ближайшем будущем. Характерные особенности: много предыдущих сессий и просмотров страниц; относительно короткий (полтора дня) интервал между сессиями; появился на сайте два месяца назад
- С – посетитель, который вряд ли вернётся на сайт. Особенности: единственная короткая сессия и единственный просмотр страницы, длившийся секунды.
- B – посетитель, вероятность возврата которого близка к
средней по сайту (а в среднем посетители возвращаются на сайт не очень охотно).
Тоже единственная сессия, с единственным просмотром страницы, длившаяся 18 секунд.
Но есть и положительные факторы: использование планшета, переход на сайт
из поисковика (по видимому Google + AdWords), переход на “мейнстримовую”
страницу ($\sum$path2=other: 0).
Заключение
Proportional hazards это не единственный возможный способ моделирования потенциального возврата посетителя на сайт. У этой модели есть свои недостатки, как математические (не всегда выполняющееся предположение о пропорциональности функций риска у разных членов популяции), так и технические: при обучении необходимо, чтобы весь dataset был в памяти, так как loss вычисляется по всему набору данных. По последней причине с этой моделью невозможно использовать минибатчи, и не получится обучиться на данных крупных сайтов, которые просто не влезают в память.
Но для сайтов небольшого и среднего размера модель вполне хороша, её главный плюс это очень экономичное использование данных: во-первых, для обучения используются все данные, включая сессии, закончившиеся недавно. Традиционные модели игнорируют свежие (самые ценные) данные, используя их только для формирования целевой переменной. Во-вторых, с помощью baseline hazard автоматически моделируется динамика выживаемости любой произвольной сложности. Например, чтобы обучиться затухающей суточной сезонности, которую мы видели на графике функции риска, традиционным методикам машинного обучения потребовалось бы очень немаленькое количество данных.
